Etiquetas

Aplicaciones del Calculo Integral -Trabajo[J]

 


Aplicaciones del Calculo Integral 

Concepto de Trabajo




Si una fuerza constante $F$ actúa sobre un objeto desplazándolo una distancia $x$, a lo largo de una línea recta, y la dirección de la fuerza coincide con la del movimiento, entonces el trabajo realizado $W$ se expresa como el producto de la fuerza $F$ por el camino recorrido.

Es decir: $W=F\cdot x$.

Cuando la fuerza no es constante, por ejemplo, cuando se contrae o estira un resorte, el trabajo no se puede expresar en forma tan simple.

Consideremos una partícula $P$ que se desplaza sobre el eje $x$, desde el punto $(a,0)$ al punto $(b,0)$ por medio de una fuerza $f=F(x),\;x\in[a,b]$.

Dividamos el segmento $[a,b]$ en $n$ partes arbitrarias de longitudes $\Delta x_1,\Delta x_2,\dots,\Delta x_i,\dots,\Delta x_n$, y tomemos en cada subintervalo $[x_{i-1},x_i]$ un punto arbitrario $t_i$ como se muestra a continuación.


Si se desea levantar un objeto desde el piso hasta una altura h, se requiere de una fuerza F cuya magnitud es el peso del objeto. Para diferentes alturas, la fuerza que se requiere es la misma, es decir, la fuerza es constante. Por definición, si un objeto es desplazado una distancia D en la dirección de una fuerza constante aplicada F entonces el trabajo W realizado por la fuerza se define por: W D FD: Cuando la fuerza F y la distancia D se expresan en newtons (N) y metros (m), respectivamente, la unidad del trabajo W es el newton-metro y se llama joule (J). Cuando la fuerza F se expresa en libras y la distancia D en pies, la unidad del trabajo W es la libra-pie. 1 libra-pie = 1:36 J



Ejemplo: 

En la siguiente figura se encuentra un cuerpo en reposo sobre una superficie plana. Debido a la acción de una fuerza variable y continua F D f .x/ D x 3 C 1, cuya magnitud está dada en newtons, el cuerpo se desplaza en línea recta desde la posición a hasta la posición b. Considerando que no existe fuerza de rozamiento entre la superficie y el cuerpo, y que la fuerza actúa en el sentido del movimiento de éste, ¿Cuál es el trabajo que realiza la fuerza f .x/ para desplazar el cuerpo?


En este ejercicio la fuerza F D f .x/ D x 3 C 1 provoca que el cuerpo se desplace desde a D 0 m hasta b D 5 m, es decir, una distancia de 5 m. Considerando la definición del trabajo W (3.1) realizado por una fuerza variable f .x/, y usando la información de este ejercicio: 




Video: 























Etiquetas:

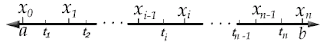
Comentarios

Publicar un comentario

Entradas populares