Áreas de Curvas

 

        ÁREAS ENTRE CURVAS 

Supongamos que f (x) y g(x) sean funciones continuas en un intervalo cerrado [a, b] tal que f (x) ≥ g(x) en [a, b]. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la siguiente figura.

Como lo hicimos antes, vamos a dividir el intervalo en el eje x y aproximar el área entre las gráficas de las funciones con rectángulos. Entonces, para i = 0, 1, 2, …, n, sea P = {x_i} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, elija un punto x_i* ∈ [x_{i − 1}, x_i], y en cada intervalo [x_{i − 1}, x_i] construya un rectángulo que se extienda verticalmente desde g (x_i*) a f (x_i*). La figura 6.2 (a) muestra los rectángulos cuando x_i* se selecciona como el punto final izquierdo del intervalo con n = 10. La figura 6.2 (b) muestra un rectángulo representativo en detalle.

La altura de cada rectángulo individual es f (x_i*) − g (x_i*) y el ancho de cada rectángulo es Δx. Agregando las áreas de todos los rectángulos, vemos que el área entre las curvas se aproxima por

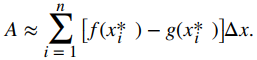
Esta es una suma de Riemann, entonces tomamos el límite cuando n → ∞ y obtenemos

Estos hallazgos se resumen en el siguiente teorema.

Ejemplo: 

Si R es la región acotada arriba por la gráfica de la función f (x) = x + 4 y abajo por la gráfica de la función g(x) = 3 − x/2 en el intervalo [1, 4], encuentre el área de región R.

Solución:

El área de la región es de 57/4 unidades².

Ejemplo 2:

Si R es la región entre las gráficas de las funciones f (x) = senx y g(x) = cosx en el intervalo [0, π], encuentre el área de la región R.

Solución:

La región se muestra en la siguiente figura.

Figura 6.1_5 La región entre estas dos curvas en el intervalo [0, π] se puede dividir en dos subregiones.

Las gráficas de las funciones se intersecan en x = π/ . Para x∈ [0, π/4], cosx ≥ senx, entonces

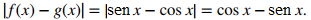
Por otro lado, para x∈ [π/4, π], senx ≥ cosx, entonces

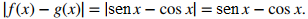
Luego

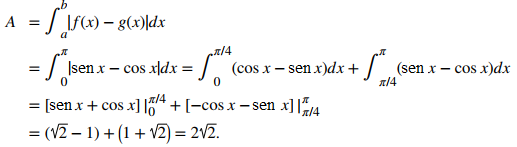
El área de la región es 2√2 unidades².

video: